Plotting and Shading Confidence Interval in Python
A confidence interval provides an estimated range of values which is likely to include the unknown parameter (such as mean) of a population when you draw samples many times from the population.
For example, if we take 100 random samples, and calculate the 95% confidence interval on each of these samples, then 95 of the 100 samples are likely to contain the population mean.
The 95% confidence interval indicates that we are 95% confident that the true population parameter will fall within the given confidence interval.
In particular, confidence intervals are useful to interpret results when the p value from the statistical test is very close to significance (e.g. 0.05).
The following examples demonstrate how to plot the confidence interval for various plots in Python.
1 Line plot (using seaborn)
We will use the lineplot function from the seaborn package (v0.13.0) for plotting the
95% confidence interval.
# import package
import seaborn as sns
# sample data
flights = sns.load_dataset("flights")
flights.head()
# output
year month passengers
0 1949 Jan 112
1 1949 Feb 118
2 1949 Mar 132
3 1949 Apr 129
4 1949 May 121
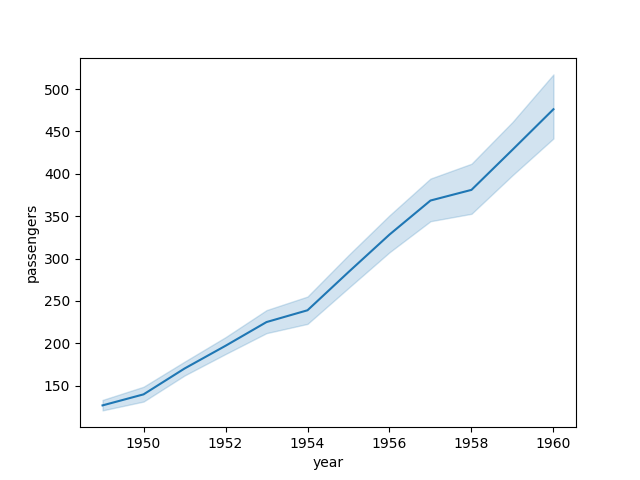
We will create a line plot between year and passengers variables.
# import package
import seaborn as sns
import matplotlib.pyplot as plt
# line plot with 95% confidence interval
sns.lineplot(data=flights, x="year", y="passengers", errorbar="ci")
plt.show()

In the above plot, the 95% confidence interval (shaded region around the line) is plotted based on the calculated mean and statistics for each year.
This shaded confidence interval represents the the range within which the true values of parameter are likely to fall.
You can also modify the confidence interval by passing the tuple to the errorbar parameter. For example, the following plot shows the
90% confidence interval.
# import package
import seaborn as sns
import matplotlib.pyplot as plt
# line plot with 95% confidence interval
sns.lineplot(data=flights, x="year", y="passengers", errorbar=("ci", 90))
plt.show()
lineplot function calculates the confidence interval if there are multiple observations for each X-axis point. By
default, it uses the bootstrap method to generate multiple samples of the provided data and calculate the confidence
interval. The confidence interval will not be plotted if there is a single value for each point on the X-axis.2 Line plot (using fill_between)
You can also use the fill_between function from matplotlib for shading the confidence interval in Python.
We will use the flights data from seaborn to calculate and shade the confidence interval.
# import package
import seaborn as sns
# sample data
flights = sns.load_dataset("flights")
flights.head()
# output
year month passengers
0 1949 Jan 112
1 1949 Feb 118
2 1949 Mar 132
3 1949 Apr 129
4 1949 May 121
Calculate the 95% confidence interval using pandas groupby function,
# import package
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# calculate upper and lower 95% confidence interval
df = flights.groupby(["year"])['passengers'].describe()[["count", "mean", "std"]].reset_index()
df["lower_ci"] = df["mean"] - 1.96*(df["std"]/np.sqrt(df["count"]))
df["upper_ci"] = df["mean"] + 1.96*(df["std"]/np.sqrt(df["count"]))
df.head()
# output
year count mean std lower_ci upper_ci
0 1949 12.0 126.666667 13.720147 118.903763 134.429570
1 1950 12.0 139.666667 19.070841 128.876323 150.457011
2 1951 12.0 170.166667 18.438267 159.734235 180.599098
3 1952 12.0 197.000000 22.966379 184.005548 209.994452
4 1953 12.0 225.000000 28.466887 208.893343 241.106657
Plot and shade the 95% confidence interval,
# import package
import matplotlib.pyplot as plt
plt.plot(df["mean"], label='Mean')
plt.plot(df["lower_ci"],'-b', label='Upper CI')
plt.plot(df["upper_ci"],'-r', label='Lower CI')
plt.fill_between(df["mean"], df["lower_ci"], df["upper_ci"], )
plt.legend()
plt.show()
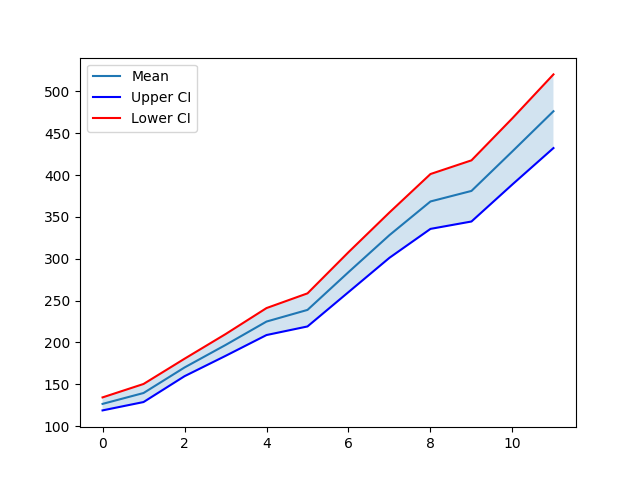
You can see that the 95% confidence interval is shaded using the fill_between function from the matplotlib.
3 Regression plot
In addition to the line plot, you can also plot the confidence interval for the regression plot (scatter plot with linear regression line).
# import package
import seaborn as sns
import matplotlib.pyplot as plt
# sample data
mpg = sns.load_dataset("mpg")
mpg.head()
# output
mpg cylinders displacement horsepower weight acceleration model_year origin name
0 18.0 8 307.0 130.0 3504 12.0 70 usa chevrolet chevelle malibu
1 15.0 8 350.0 165.0 3693 11.5 70 usa buick skylark 320
2 18.0 8 318.0 150.0 3436 11.0 70 usa plymouth satellite
3 16.0 8 304.0 150.0 3433 12.0 70 usa amc rebel sst
4 17.0 8 302.0 140.0 3449 10.5 70 usa ford torino
Create a scatter plot between weight and mpg variables, and add a regression line with 95% confidence interval
# import package
import seaborn as sns
import matplotlib.pyplot as plt
# create regression plot with confidence interval
sns.regplot(data=mpg, x="weight", y="mpg",ci=95, line_kws=dict(color="r"))
plt.show()
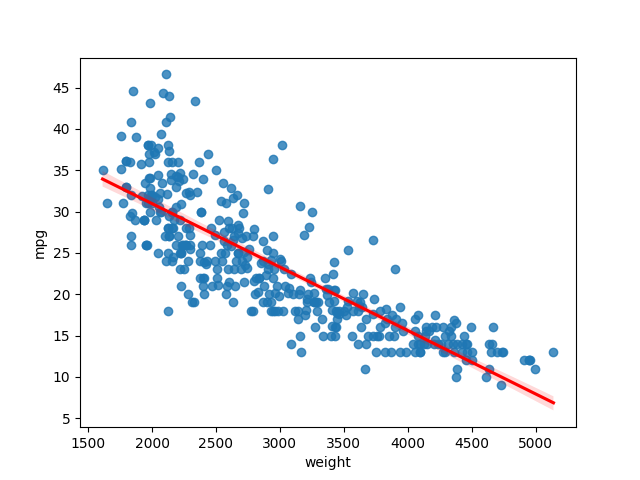
The 95% confidence interval (the shaded region around the red line) for the regression plot is calculated using the bootstrap method (the dataset is randomly resampled with a replacement for a certain number of times, and statistics are calculated from the bootstrap sampling).