How to Perform Welch's t-test in Python

1. Welch’s t-test

Welch’s t-test is a statistical method used in comparing the means of two independent groups when the assumption of equal variance between the two groups is violated.

Welch’s t-test extends the traditional two-sample t-test and is specifically designed for situations where we cannot assume equal variances between the two groups being compared.

In Python, you can perform Welch’s t-test using the ttest_ind function from scipy package. The basic syntax of this function is as follows:

# import package
import scipy.stats as stats

# Welch's t-test
stats.ttest_ind(x, y, equal_var=False, alternative="two-sided")

Where,

The following example illustrates how to perform Welch’s t-test in Python with an example dataset.

2. Welch’s t-test hypothesis

Null Hypothesis (H0): Means of the two groups are equal

Alternative Hypothesis (H1): Means of the two groups are not equal

3. Perform Welch’s t-test Python

3.1 Sample dataset

Suppose we collect the data for plant heights of two genotypes (genA and genB) after fertilizing them.

We want to check whether the application of fertilizer significantly affects plant heights in two genotypes.

genA = [36, 39, 32, 37, 70, 85, 70, 39, 45, 35]
genB = [38, 31, 38, 36, 45, 35, 36, 36, 39, 35]

3.2 Test hypothesis

Our objective is to test the Null hypothesis whether the mean of plant heights in two groups (genA and genB) is the same against the alternative hypothesis that they differ significantly.

Null Hypothesis (H0): Means of plant heights of the two genotypes are equal

Alternative Hypothesis (H1): Means of plant heights of the two genotypes are not equal (two-sided)

3.3 Assumption of equal variances

Before performing the Welch’s t-test, it is necessary to check the assumption of equality of variances between the two groups.

To check the assumption of equality of variances, you can either use the Bartlett test or visualize the group means using the boxplot.

Let’s perform the Bartlett test,

# import package
import scipy.stats as stats

# perform Bartlett test
stats.bartlett(genA, genB)

BartlettResult(statistic=16.989618011541815, pvalue=3.758477274561406e-05)

As the p value obtained from the Bartlett test is less than the significance level (0.05), we can reject the null hypothesis of equal variance.

In addition, you can also use a boxplot to visualize the equality of variances. You can check the spread of the data to conclude the equality of variances.

# import package
import matplotlib.pyplot as plt

# create boxplot 
plt.boxplot([genA, genB], labels=['genA', 'genB'])
plt.show()

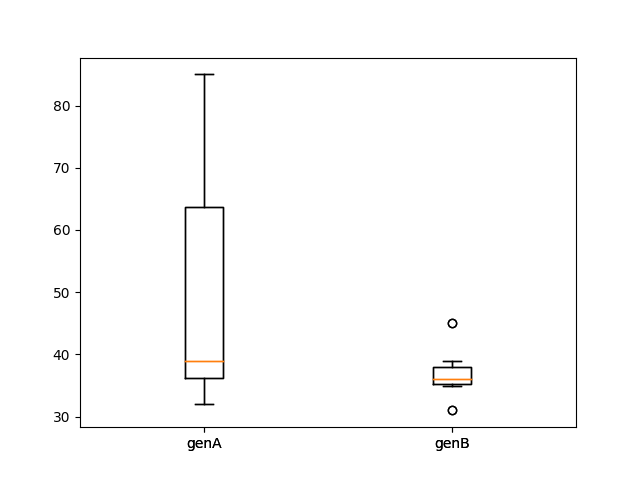
The boxpot clearly shows that the spread of the data is highly different for the genA group than the genB group.

Hence, based on the Bartlett test and boxplot, we can assume that the variances are not equal in the two groups of plant genotypes.

As the variances are not equal, we should perform Welch’s t-test to compare the means of plant heights for the genA and genB genotype groups.

3.4 Perform Welch’s t-test

Let’s perform the Welch’s t-test in Python,

# import package
import scipy.stats as stats

# Welch's t-test
stats.ttest_ind(genA, genB, equal_var=False)

# output
Ttest_indResult(statistic=1.9626942340799944, pvalue=0.0791060979778394)

The p value and t statistics obtained from Welch’s t-test are 0.0791 and 1.9626, respectively.

As the p value is non-significant (p > 0.05), we fail to reject the null hypothesis that the mean plant heights of the two genotypes are equal.

We can conclude that the plant height of genotype A (genA) and genotype B (genB) groups are not significantly different.